Annulus Calculator
| r1 = | |
| r2 = | |
| Units: | |
| C1 = | 0 |
| C2 = | 0 |
| A1 = | 0 |
| A2 = | 0 |
| A0 = | 0 |
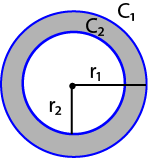
r1 = outer radius
r2 = inner radius
C1 = outer circumference
C2 = inner circumference
A1 = area of circle of r1
A2 = area of circle of r2
A0 = shaded area
The online annuluses calculator to find the area, circumference and radius of an annulus. When you know two known variable, then select from the droplist, calculate the other 5 unknowns.
Annulus Formulas:
Given r1 and r2:
C1 = 2πr1
C2 = 2πr2
A1 = πr12
A2 = πr22
A0 = A1 - A2.
Given r1 and C2:
r2 = C2 / 2π
C1 = 2πr1
A1 = πr12
A2 = πr22
A0 = A1 - A2.
Given r1 and A2:
r2 = √(A2 / π)
C1 = 2πr1
C1 = 2πr2
A1 = πr12
A0 = A1 - A2.
Given r2 and C1:
r1 = C1 / 2π
C2 = 2πr2
A1 = πr12
A2 = πr22
A0 = A1 - A2.
Given C1 and C2:
r1 = C1 / 2π
r2 = C1 / 2π
A1 = πr12
A2 = πr22
A0 = A1 - A2.
Given C1 and A2:
r1 = C1 / 2π
r2 = √(A2 / π)
C2 = 2πr2
A1 = πr12
A0 = A1 - A2.
Given r2 and A1:
r1 = √(A1 / π)
C1 = 2πr1
C2 = 2πr2
A2 = πr22
A0 = A1 - A2.
Given C2 and A1:
r1 = √(A1 / π)
r2 = C2 / 2π
C1 = 2πr1
A2 = πr22
A0 = A1 - A2.
Given A1 and A2:
r1 = √(A1 / π)
r2 = √(A2 / π)
C1 = 2πr1
C2 = 2πr2
A0 = A1 - A2.
Given r1 and A0:
C1 = 2πr1
A1 = πr12
A2 = A1 - A0
r2 = √(A2 / π)
C2 = 2πr2.
Given r2 and A0:
C2 = 2πr2
A2 = πr22
A1 = A0 + A2
r1 = √(A1 / π)
C1 = 2πr2.
Given C1 and A0:
r1 = C1 / 2π
A1 = πr12
A2 = A1 - A0
r2 = √(A2 / π)
C2 = 2πr2.
Given C2 and A0:
r2 = C2 / 2π
A2 = πr22
A1 = A0 + A2
r1 = √(A1 / π)
C1 = 2πr1.
Given A1 and A0:
A2 = A1 - A0
r1 = √(A1 / π)
r2 = √(A2 / π)
C1 = 2πr1
C2 = 2πr2.
Given A2 and A0:
A1 = A0 + A2
r1 = √(A1 / π)
r2 = √(A2 / π)
C1 = 2πr1
C2 = 2πr2.