InterQuartile Range (IQR) Calculator

Enter Numbers:
IQR:
Total Numbers:

In descriptive statistics, the interquartile range (IQR), also called the midspread or middle fifty, is a measure of statistical dispersion, being equal to the difference between the upper and lower quartiles, IQR = Q3 - Q1. In other words, the IQR is the 1st Quartile subtracted from the 3rd Quartile; these quartiles can be clearly seen on a box plot on the data. It is a trimmed estimator, defined as the 25% trimmed mid-range, and is the most significant basic robust measure of scale.

Data set in a table

i x[i] Quartile
1 102
2 104
3 105 Q1
4 107
5 108
6 109 Q2
(median)
7 110
8 112
9 115 Q3
10 116
11 118

For the data in this table the interquartile range is IQR = 115 - 105 = 10.

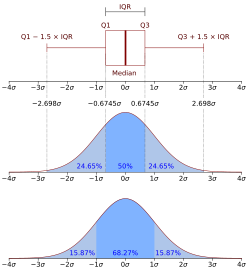
Boxplot (with an interquartile range) and a probability density function of a Normal N(0,σ2) Population
calculator.cpu.com.cn provides you helpful and handy calculator resources.
Category Loan Tax Interest Investment Profit & Loss Credit and Debt Planning Algebra Calculus Statistics Matrix Number Plane Geometry Solid Geometry Trigonometry Construction Analytic Geometry Math graphing Color Converter Numeral system Unit Energy Temperature Power Frequency Charge Voltage Lighting Classic Physic Electronic Engineering Chemistry Electrical Date Time Commemorative days Observance days Health and medicine Family and Fun Weather Webmaster tools