Calculator.cpu.com.cn - Your Calculator Resources Online!

The Standard Deviation Calculator to calculate common measure of the spread of a data set, it is a data analysis. The calculator could give you No.of Inputs, Mean, Standard Deviation(SD), Population Standard Deviation(PSD), Variance(SD), Variance(PSD) of a given input values of data set.

Standard Deviation Formula

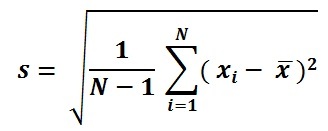
Population SD formula

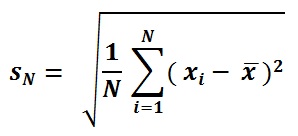
Variance formula

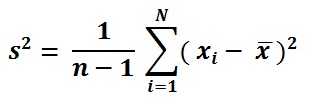
Mean formula

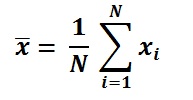
For example, when given a data set 5,20,40,80,100, the result will be:

Total Inputs(N) =(5,20,40,80,100)
Total Inputs(N)=5
Mean(xm)= (x1+x2+x3...xN)/N 
Mean(xm)= 245/5
Means(xm)= 49
-------------------------------------------
SD=
sqrt(1/(N-1)*((x1-xm)^2+(x2-xm)^2+..+(xN-xm)^2))
=sqrt(1/(5-1)((5-49)^2+(20-49)^2+(40-49)^2+(80-49)^2+(100-49)^2))
=sqrt(1/4((-44)^2+(-29)^2+(-9)^2+(31)^2+(51)^2))
=sqrt(1/4((1936)+(841)+(81)+(961)+(2601)))
=sqrt(1605)
=40.0625

Variance=SD^2
Variance=40.0625^2
Variance=1605
-------------------------------------------
PSD=
sqrt(1/(N)*((x1-xm)^2+(x2-xm)^2+..+(xN-xm)^2))
=sqrt(1/(5)((5-49)^2+(20-49)^2+(40-49)^2+(80-49)^2+(100-49)^2))
=sqrt(1/5((-44)^2+(-29)^2+(-9)^2+(31)^2+(51)^2))
=sqrt(1/5((1936)+(841)+(81)+(961)+(2601)))
=sqrt(1284)
=35.8329

Variance=SD^2
Variance=35.8329^2
Variance=1284